総論	国語	社会	算数	理科	生活	音楽	図工	家庭	体育
平成15年度
平成16年度

トップページへ 　　　　　

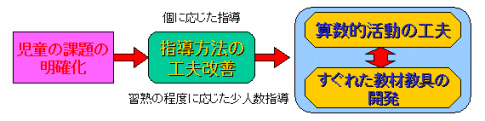
前項で述べたように、各校でのこれまでの授業改善の努力によって、正答率が全般的に伸びてきている。にもかかわらず、特定の誤答に関して言えば、依然として同様の比率でまたは、増加の傾向で低位の児童が存在する。今後は、これらの児童に焦点を当てた指導を進めることが大変重要であると考える。 　　そのためには、まず課題を明確にすることは当然である。その上で、指導方法の工夫改善を進めるわけであるが、その視点としては、定着・習熟以前の作業的・体験的な活動を取り入れた算数的活動を工夫していくことがとりわけ大切である。 　　算数的活動は、数量や図形についての感覚を豊かにするとともに、基礎的な知識と技能を身に付けるためには欠くことのできない活動である。また、この算数的活動の成否にとって優れた教材教具の存在が重要な要素となる。 　　そこで、優れた教材教具を活用した算数的活動の実践例を紹介する。

(１)　6年／分数のかけ算、わり算の学習で、「面積図」を使った算数的活動例
※　ノートの記述例へ			※　ノートの記述例へ	動画が見られます。
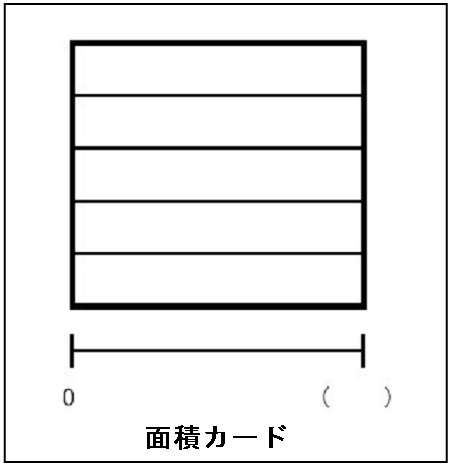
児童にとって、分数÷分数の理解は大変困難な内容である。これは割ることの意味が具体的にイメージしにくいことも一因であると考えられる。教科書では、線分図や面積図を使った考え方が載っており、教師の指導・解説には活用されてはいるが、児童自身が考える時の手がかりとして活用しているかどうかは疑問である。 　　そこで、この面積図を、児童自身が分数の乗法・除法の式の意味を考える手がかりとして使い、より深く理解できるようにするというのがこの実践例のねらいである。 　　そのためには、下図のような面積図のプリントを用意し、分数のかけ算の学習の当初から活用することにした。 　　児童は、つねにこのプリントの面積図を使いながら、式の意味を考える学習を続けることで、一般に理解が難しいとされる分数のわり算についても、その考え方を面積図を使って説明できるようになった。 　　　　　　　　　　　　　　　　　　　　　　※　ノートの記述例へ
＜指導上の工夫＞ �@ ノートに貼れるサイズの面積図のプリント（カード）をたくさん用意し、いつでも使えるようにしておく。 �A 面積図を使って式の意味を考える時間をしっかり確保する。 �B 単元を通して、一貫して面積図を使って考えることに慣れさせる。 �C 児童自身が考え方を書いた面積図は、その都度ノートに貼り、考え方を文章でで書くように指導する。 �D 発表ボードを使って、それぞれの児童の考え方を友達の前で発表する機会を随時設ける。				動画が見られます。
「数学的な考え方」を育成するためには、考える際の足がかりとなる材料と十分な時間を与えることが必要である。しかも、その材料に慣れると同時に、考えること自体にも慣れさせることも必要である。こうした条件を念頭におき、「数学的な考え方」を育成する新たな算数的活動を創造していくことが求められている。

(２)　４年／面積の学習で、「1�uが体感できる教具」を使った算数的活動例
１�uの指導をするとき、いろいろと工夫を凝らし教材を開発された先生は多いと思う。 　ここで紹介する教具は、材料としてゴミ袋を使ったというだけでなく、細部に渡って考案者のアイデアがたくさん付加されている点でも優れている。教具の特性等の紹介は省略（詳細はセンターHPに）することとして、活動例をいくつか紹介する。
ＮＯ 活動内容 活動のねらい �@ １�uをつくる活動 辺の長さを測ったり切ったり、直角を意識したりする活動を通して、１�uの広さを体感する。 �A １�uの広さに何人のれるか確かめる活動 床の上に１�uの教具を広げ、その上にできるだけたくさんの友達がのる活動を通して、１�uの広さを体感する �B 教室や体育館に１�uの教具を敷き詰めて広さを確かめる活動 まず、教室（または体育館）の広さは何�uかを予想（根拠も述べさせるのが大事）し、実際に１�uの教具を敷き詰めて広さを確認するとともに、単位量をとしての１�uを体感する。 �C １立方メートル（体積）のかさを確かめる活動 この教具の上下辺に１ｍものさしを入れたもの6枚を組合わせて、協力しながら１立方メートル（体積）のかさを作り、中に入ったりする活動を通して１立方メートル（体積）のかさを体感する。
※ 画面をクリックすると拡大
上のスライドは、ＩＴＥＣ／学校支援／小学校／「算数の教材教具集」で見ることができます。
「数学的な考え方」を育成するためには、考える際の足がかりとなる材料と十分な時間を与えることが必要である。しかも、その材料に慣れると同時に、考えること自体にも慣れさせることも必要である。こうした条件を念頭におき、「数学的な考え方」を育成する新たな算数的活動を創造していくことが求められている。

(３)　４年／三角形の学習で、「二等辺三角形の作図法を考えるソフト」を使った算数的活動例
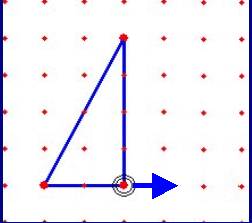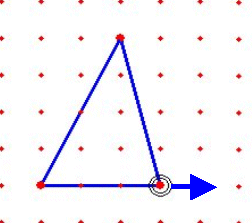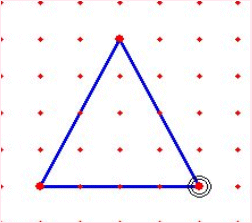
図形の作図法は、児童自らが考えるというよりは、知識や技能として教え、習熟のために練習を繰り返すという場合が多い。しかし、作図の方法は道理にかなっており、その方法を考えることは図形についての理解を深める上で有効であると考える。 　とはいっても、何も足がかりなしに児童に考えさせるには無理がある。そこで、その足がかりになる「動きのある教材」をもとに、児童自身が考える場を設定しようというのが、ここでの算数的活動例である。 　この動画ソフトは、下の図にあるように「等しい２辺が交わる点を見つけることがポイントであることに気付く」そして、「その点を、決定する作図の方法を考える」ことがねらいである。			画面の前で、動作化しながら 二等辺三角形の作図法を説明する児童	動画が見られます。
このソフトを使った指導の中で、画面を見ながら、動作化をするなどして真剣に考える児童の姿が見られた。 　 このようにして身につけた知識や技能は、確実な定着につながると考えられる。教師自身が「これは教え込む内容」と考えている内容についても今一度見直し、適切な教材と時間設定によって有効な算数的活動となりえないかを点検することが大切ではないだろうか。

(４)　４年／三角形の学習で、「ジオボードソフト」を使った算数的活動例
ここでは、ジオボードソフトを使って、図形についての豊かな感覚を育てる実践例を紹介する。 ジオボードについては、かなり一般的になってきたが、まだ聞いたことがないという先生方のために、まずは、ジオボードとは何かということを紹介する。
「ジオボードは，アメリカで広く使われている学習具で、図形領域の学習を中心にもちいられます。実物は、正方形の板にペグと呼ばれる釘が打ち付けてあり、そこに輪ゴムをかけて形を作ります。ここにあるジオボードは、アメリカのNCTMのサイトにあるもので、マウスを使って実物のジオボードと同様な活動ができるようになっています。」 （www.e-sensei.ne.jp/~Innternet Math/nctm/goeboard.htmlより引用） (※引用文中「NCTM」とはNational Coun-cil of Teachers of Mathematicsで、日本語では全米数学教師協議会と呼ばれているアメリカ最大の数学を教える先生方の研究組織)				動画が見られます。
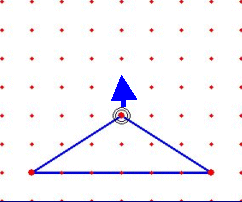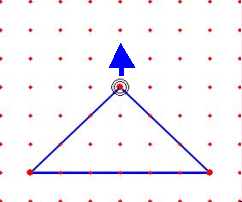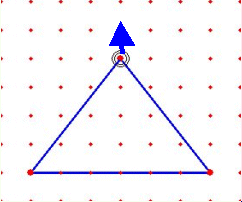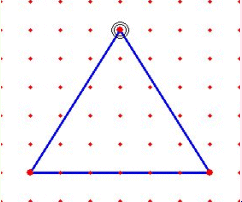
図形の構成や図形の性質について学習するためには、その土台として具体物の操作体験が重要である。その体験を通して身についた感覚をもとにして、図形についての理解が深まっていくと考えられる。(2)-ウ「新たな課題と習熟度に応じた少人数指導への期待」で示したような誤答をする児童の多くは、このような感覚が十分に育っていないと考えられないだろうか。 　そこで、これらの児童には、図形に関する新たな学習を進めることと並行して、 短時間に効率的な体験ができる工夫が必要だと考える。それには、ＩＴを活用した学習が有効であり、今後各校でハード面の整備が進むと益々活用の幅が広がることが期待できる。 　ジオボードソフトを活用した実践で、次のような事例が見られた。 　二等辺三角形の作図の学習の結果、児童は、定規とコンパスを使って二等辺三角 形が正しくかけるようになった。そこで、ジオボードソフトを使って二等辺三角形をたくさんかく活動をさせたところ、明らかに二等辺三角形の特徴を感覚としてとらえられていないと考えられる児童が何人か見つかったのである。 　このことから言えることは、操作の仕方や図形の特徴などを技能や知識として覚 えることはできても、それが図形についての感覚を育てることとは直接は結び付いていないということである。 　また一方で、ジオボードソフトを使って、二等辺三角形の作図法を見つけ出した 児童もいる。下の２例は、ジオボードならではの作図法であり、二等辺三角形に対する理解がより深まったと考えられる。 　　　　　　　　　　　　　　　　　　　　　※　実際にジオボードを使った児童の事例へ

トップページへ ページの先頭へ戻る