| 総論 | 国語 | 社会 | 算数 | 理科 | 生活 | 音楽 | 図工 | 家庭 | 体育 | |
| 平成15年度 | ||||||||||
| 平成16年度 |


![]()
| 実 践 例 目 次 ※ 各項目にリンクします | |||||||
|---|---|---|---|---|---|---|---|
| Ⅰ 児童の学力状況をどのように して把握するのか |
Ⅱ 習熟の程度に応じた少人数 指導のあり方について |
Ⅲ 算数的活動の工夫 | Ⅳ 指導と一体化した 評価の工夫 |
||||
| (1) |
度数分布グラフ(小学校基礎学力診断テスト)等から少人数指導の方針を立てる例 | (1) |
課題によるグループ分けとコース設定の例 | (1) |
6年/分数のかけ算、わり算の学習で、「面積図」を使った算数的活動例 | ||
| (2) |
「こべつ~る」とレディネステストから学力の状況を把握する例 | (2) | 学習コースを自ら選ぶ力の育成をめざす例 | (2) | 4年/面積の学習で、「1㎡が体感できる教具」を使った算数的活動例 | ||
| (3) |
児童の課題にあった指導方法の工夫の例 | (3) |
新たな課題と習熟の程度に応じた少人数指導への期待 | (3) | 4年/三角形の学習で、「二等辺三角形の作図法を考えるソフト」を使った算数的活動 | ||
| (4) | 4年/三角形の学習で、「ジオボードソフト」を使った算数的活動 | ||||||
| (1) 度数分布グラフ(小学校基礎学力診断テスト)から少人数指導の方針を立てる例 | |
 |
|
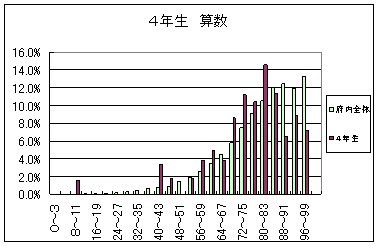
| ある小学校の4年生算数のテスト結果の度数分布は下のようなグラフとなった。 平均正答率は府の平均を下回り、典型的なふたこぶ型の分布が見られるのが特徴である。 そこで、校内での協議の結果、習熟の程度にあわせてグループを編成し、各グループの課題に応じた指導方法を工夫して基礎学力の向上を目指すことにした。 |
| (2) 「こべつ~る」とレディネステストから学力の状況を把握する例 |
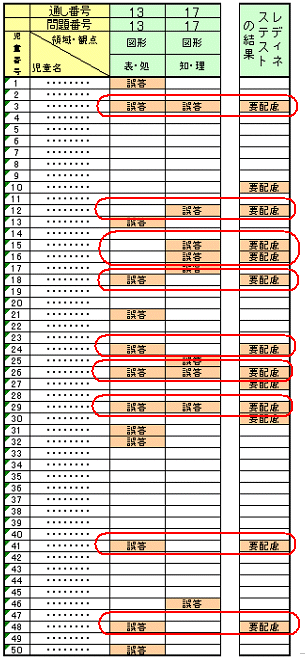
| この小学校では、4年生の「三角形」の学習をするにあたって、小学校基礎学力診断テストの図形に関連する問題の解答状況を確認した。 さらに、レディネステストを行い、その結果と先の診断テストの結果を見比べた。 小学校基礎学力診断テストの13番は、「直角三角形の作図(図形領域、表現処理)の問題」で、17番は「長方形の判別(図形領域、知識・理解)の問題」である。レディネステストでは、「図形(正方形、直角三角形、長方形)の名称と性質及びその判別」、「箱の形の面・辺・頂点の数」、「もよう作りの理解と習熟」をテストした。 その結果、右表のように、レディネステストで課題があると考えられる児童の大部分が小学校基礎学力診断テストでも誤答していることが分かった。(図) これらの児童の課題として次の3点が考えられる。 |
 「こべつ~る」のデータを印刷したもの ※ 画面上でクリックすると拡大 |
 |
|---|---|
| 個人情報保護のため 実際のデータを特定 ⇒ できないようにしてあります |
|
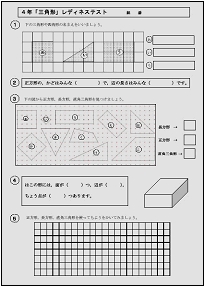 レディネステスト拡大 |
| (3) 児童の課題にあった指導方法の工夫の例 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||
| 大切なことは、明らかになった児童の課題に応じて、指導の手立てを考えることである。表中のA・Bは、児童の学習状況(課題)をもとに仮にA群・B群と2つに分けたのであって、それが直接2つのコース学習につながるものではないことに留意する必要がある。 | |||||||||||
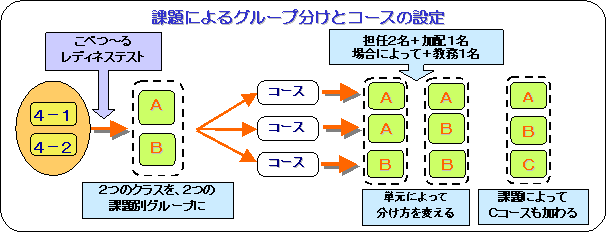
| (1) 課題によるグループ分けとコース設定の例 | |||||
 |
|||||
| (1)のウで示したように、児童の学習状況(課題)によってA群・B群と分けたとき、その人数の分かれ具合は、その時々の児童実態によって変わってくる。 つまり、A群の児童が多い場合もあれば、その逆もある。また、それぞれの群の指導の手立てと照らして考えたとき、何人程度の集団が適当であるかということも考慮しなければならない。 さらに、指導可能な教師の人数や学習場所等の条件もある。 |
|||||
| これらのことを総合的に考え、学習コースを設定することが必要となる。 要するに、ここでもっとも大切なことは次の2点である。 |
|||||
|
|||||
| (2) 学習コースを自ら選ぶ力の育成をめざす例 | |||||
|---|---|---|---|---|---|
| 「学習コースを児童自らが選ぶ」方法をとっている学校は多い。しかし、その目的を明確にして取り組んでいるであろうか。ただ単に、「児童の主体的な選択」ということを強調するにとどまっていないだろうか。
「学習コースを児童自らが選ぶ」ということは大きな意義のあることである。しかもそれを意識的に取り組むことで、次のような効果が期待できる。 |
|||||
|
|||||
| 以上のような効果を意図し、目的として明確に掲げ取り組んでいくことが重要である。しかし、これらの効果は、「好きなコースを選びなさい」式のやり方では期待できない。 | |||||
|
|||||
| つまり、このようなていねいな指導によってはじめて、大きな効果が生まれるといえるのである。 「京都夢・未来校」において、「児童は本当に自分にあったコースを選べるのだろうか」という論議がなされてきた。そこでの結論は、「はじめの内は、気の合う友だちと一緒など、他の要素で選択する児童もいるが、適切な指導によって、徐々に自分にあったコースを選ぶ力が育ってくる。そのことによって意欲的な学習が一層進むようになる。」ということである。 限られた時間の中で、レディネステストやオリエンテーション、ガイダンスに大きな時間を割くことは困難な面が多い。大切なのは、これらの重要性を十分に理解し、短時間の中に、オリエンテーション的な指導やガイダンス的な指導をいかに効果的に組み込むかを工夫することである。 |
| (3) 新たな課題と習熟の程度に応じた少人数指導への期待 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 小学校基礎学力診断テストの結果を詳しく分析してみると、新たな課題が見えてきた。それは、全般に正答率が上昇している問題であっても、一部の誤答については、それを選択する児童の比率が減少していないという課題である。この課題は、4年生にも6年生にも見られる課題である。
たとえば、下の表は、6年生の小学校基礎学力診断テストに出題された問題の一部について、正答と誤答の選択率の変化を表したものである。それぞれの問題は、平成14年度から平成16年度までの類似問題である。表からも分かるように3問とも正答率は年々上昇しているが、太字で示した誤答を選択した児童は減少していないどころか、増加している場合もあることが分かる。 正答率の上昇を、授業改善の結果と考えた場合、この改善方法では指導しきれない児童がいると考えなければならないだろう。そういう意味からも、習熟の程度に応じた少人数指導を、これらの層の児童に基礎学力をつけていくための有効な手立てとして捉え、実践していくことが必要である。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 実 践 例 目 次 ※ 各項目にリンクします | |||||||
|---|---|---|---|---|---|---|---|
| Ⅰ 児童の学力状況をどのように して把握するのか |
Ⅱ 習熟の程度に応じた少人数 指導のあり方について |
Ⅲ 算数的活動の工夫 | Ⅳ 指導と一体化した 評価の工夫 |
||||
| (1) |
度数分布グラフ(小学校基礎学力診断テスト)等から少人数指導の方針を立てる例 | (1) |
題によるグループ分けとコース設定の例 | (1) |
6年/分数のかけ算、わり算の学習で、「面積図」を使った算数的活動例 | ||
| (2) |
「こべつ~る」とレディネステストから学力の状況を把握する例 | (2) | 学習コースを自ら選ぶ力の育成をめざす例 | (2) | 4年/面積の学習で、「1㎡が体感できる教具」を使った算数的活動例 | ||
| (3) |
児童の課題にあった指導方法の工夫の例 | (3) |
新たな課題と習熟の程度に応じた少人数指導への期待 | (3) | 4年/三角形の学習で、「二等辺三角形の作図法を考えるソフト」を使った算数的活動 | ||
| (4) | 4年/三角形の学習で、「ジオボードソフト」を使った算数的活動 | ||||||