

| Ⅰ 算数科 学習指導案 1 対象 2 単元 3 単元目標 4 単元の評価規準 5 単元の指導と評価の計画 6 各教科の教材問題 7 本時の目標 8 本時の展開 Ⅱ 資料 資料1 学習指導要領算数の目標 資料2 算数的活動 資料3 算数的活動の意義 資料4 発展的な学習と補充的な学習 資料5 自己診断票 |
| Ⅰ 算数科 学習指導案 |
| 算数科 学習指導案 | ||||||||||||||||||||||||||||||||||||||||||||
| 1 対 象 第6学年 |
||||||||||||||||||||||||||||||||||||||||||||
| 2 単 元 割合を使って (啓林館6年下P.36~39) |
||||||||||||||||||||||||||||||||||||||||||||
3 単元目標
|
||||||||||||||||||||||||||||||||||||||||||||
| 4 単元の評価規準 |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
| 5 単元の指導と評価の計画 | ||||||||||||||||||||||||||||||||||||||||||||
|
【関】関心・意欲・態度,【考】数学的な考え方,【表】表現・処理,【知】知識・理解 |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
| 6 各時間の教材問題 (啓林館6年下) | ||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
| 7 本時の目標 第2/5時 | ||||||||||||||||||||||||||||||||||||||||||||
| ・割合の和を考えることのよさに気づき、それを用いようとする。(関心・意欲・態度) ・全体を1として、部分と部分の割合の和を考えて、問題の解決ができる。(数学的な考え方,表現・処理) |
||||||||||||||||||||||||||||||||||||||||||||
| 8 本時の展開 第2/5時 | ||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||
学習指導要領算数の目標
数量や図形についての算数的活動を通して、基礎的な知識と技能を身に付け、
日常の事象について見通しをもち筋道を立てて考える能力を育てるとともに、活動の楽しさや数理的な処理のよさに気付き、進んで生活に生かそうとする態度を育てる。
-小学校学習指導要領より-
算数的活動
児童が目的意識をもって取り組む算数にかかわりのある様々な活動の総称。
作業的・体験的な活動など手や身体を使った外的な活動を主とするが、思考活動など内的な活動を主とするものも含まれる。
・手や身体等を使って、ものを作る活動
・教室の内外において、各自が実際に行ったり確かめたりする活動
・身の回りにある具体物を用いた活動
・実態や数量などを調査する活動
・概念、性質や解決方法などを見付けたり、つくり出したりする活動
・学習したことを発展的に考える活動
・学習したことを様々な場面に応用する活動
・算数のいろいろな知識、あるいは算数の様々な学習で得た知識などを総合的に用いる活動
-小・中学校授業改善ハンドブック(H12,3月/京都府教委)より-
算数的活動の意義
・算数の授業を児童の活動を中心とした主体的なものとする。
・算数の授業を児童にとって楽しいものとする。
・算数の授業を児童にとって分かりやすいものとする。
・算数の授業を児童にとって感動のあるものとする。
・算数を日常生活や自然現象と結び付いたものとする。
・算数の授業を創造的、発展的なものとする。
・算数と他教科等を関連させる活動を構想しやすいものとする。 -小・中学校授業改善ハンドブック(H12,3月/京都府教委)より-
| 発展的な学習 学習指導要領に示す内容を身に付けている児童生徒に対して、個に応じた指導の充実を図る観点から、児童生徒の興味・関心等に応じて、学習指導要領に示す内容の理解をより深める学習を行ったり、さらに進んだ内容についての学習を行ったりするなどの学習指導であるといえる。児童生徒の理解や習熟の状況等に応じ、指導内容を適宜工夫することが求められているが、その際、学習指導要領に示す内容と全く関連のない学習や児童生徒の負担過重となるような指導にならないようにすることに留意する必要がある。 |
補充的な学習 全ての児童生徒が基礎・基本を確実に身に付けることができるようにすることが重要であり、補充的な学習とは、児童生徒の理解や習熟の状況等に応じ学習指導要領に示す基礎的・基本的な内容の確実な定着を図るために行う学習指導であるといえる。各学校にあっては、個別指導やグループ別指導、繰り返し指導、ティームティーチングなど様々な指導方法や指導体制の工夫改善を進め、当該学年で学習する内容の確実な定着を図ることが重要である。 |
| -小・中学校授業改善ハンドブック(H15.3月/京都府教委)より- | |
※ クリックすると、自己診断票についての解説が見られます。
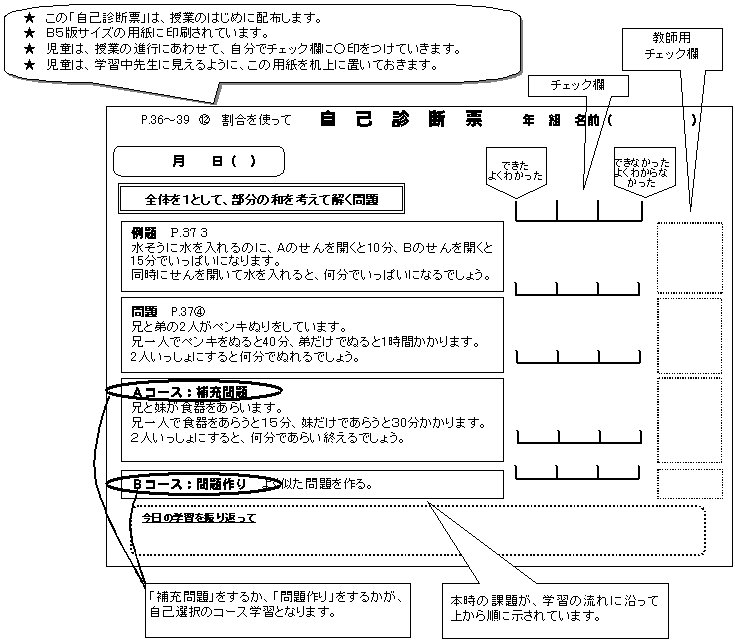
|